スポットのサイズとビームウエスト
この計算機は、入力したレンズ、波長、およびその他のパラメーターでのビーム径に基づいて、レーザースポットサイズとレーザービームウエスト値を示します。
レーザービームのウエストとスポットサイズの計算機はどのように機能しますか?
まず、収束レンズを通過するガウシアンレーザービームを考慮します。ビームは収束し始め、最終的に最大濃度のポイントに到達します。この時点で、ビーム径は最小になります。この直径を「スポットサイズ」と呼びます (「ビームウエスト」も同じ概念ですが、一般的には半径を指します)。腰を過ぎると、ビームは再び発散し始め、さらに進むにつれて幅が広がります。Z軸上の腰の位置は、特に焦点距離に依存します。本質的に、焦点距離は、レンズが光を収束または発散させる強さを示す値です。したがって、レンズが収束するほど、焦点距離は短くなり、ウエストはレンズに近づきます。したがって、ビームウエストからの距離が分かれば、ビームのサイズを決定することができます。また、被写界深度と呼ばれるものは、ビームウエストを中心とした特定の距離であり、ビームの直径はスポットサイズに比べてかなり小さくなります。また、レイリー距離の2倍です。レイリー長は、ビーム半径がウエストの半径の√2倍以下になる距離として定義されます。そのため、焦点距離が入射ビームサイズに比べて小さい場合、被写界深度は小さくなる傾向があり、逆もまた同様です。最後に、M²は品質係数に対応します。基本的には、完全に成形された理論上のTEM₀₀ガウシアンビームと比較した場合に、ビームがどの程度良好に動作するかを測定したものです。「1」の値は完全であると見なされ、その値から離れているほど、完全ではありません。
クリックして拡大する
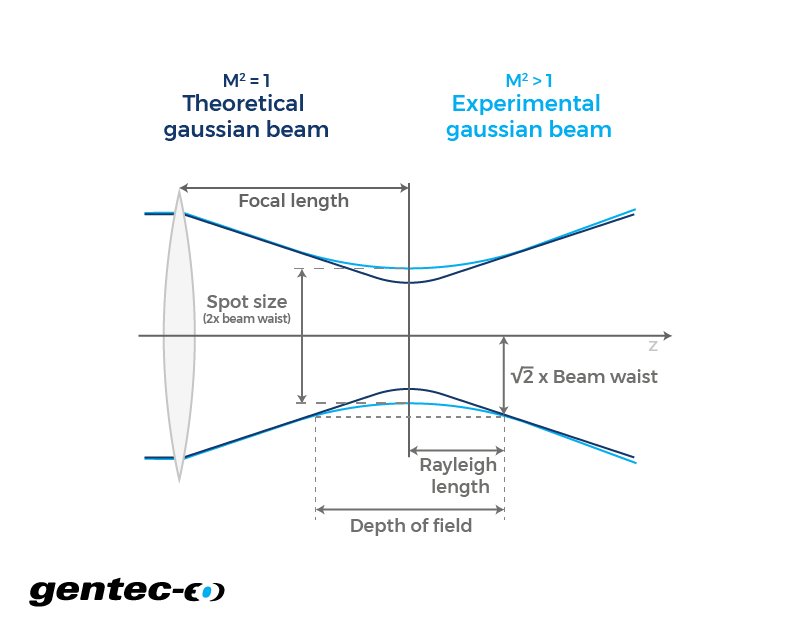
スポットサイズ、ビーム径、被写界深度の数式
ここでは、レーザービームがレンズを通過すると、均一な等方性連続媒質を永久に通過すると仮定されます。また、レーザーは1つの特定の波長のみを放射し、TEM₀₀ガウシアンビームとして表すことができると仮定されています。ビームに加えて、レンズは完璧で薄いと考えられています。そのため、表面に凹凸がなく、焦点距離は表面全体で同じです。私たちの計算は、ヘルムホルツ方程式の近軸近似と薄レンズ近似から得られます。また、入射ビームはレンズ上で完全にコリメートされていると見なされます。したがって、z軸上のウエスト位置は焦点と一致し、レンズから焦点距離にあります。最後に、これらの式は遠方界でのビーム径を正確に計算できません。その場合、最初の直径が正確 (0) で、焦点面に直接ある発散計算機を使用する必要があります。
参照:Saleh, B. E. A., & Teich, M. C. (2007).Fundamentals of Photonics (2nd ed.).Wiley-Interscience.
右クリックでコピーする
右クリックでコピーする
右クリックでコピーする