Spot size and beam waist
This calculator gives you the laser spot size and laser beam waist values based on the beam diameter at lens, wavelength, and other parameters you input.
How does the laser beam waist and spot size calculator work?
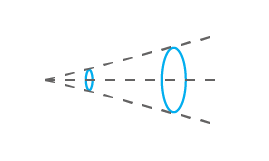
First, consider a Gaussian laser beam that is going through a converging lens. The beam will start to converge and eventually, will reach a point of maximum concentration. At this point, the beam diameter will be at its minimum. This diameter is what we call the "spot size" (the "beam waist" is the same concept, but would generally refer to the radius). Past the waist, the beam begins to diverge again and the further it goes the wider it becomes. The waist position on the z axis depends, amongst other things, on the focal length. Essentially, the focal length is a value that indicates how strongly a lens makes light converge or diverge. So, the more converging a lens is, the smaller the focal length is and the closer to the lens the waist will be. Therefore, it is possible to determine the size of the beam if the distance from the beam waist is known. Also, what is called depth of field is a specific distance, centered around the beam waist, for which the beam has an appreciably small diameter compared to its spot size. It is also double the Rayleigh distance. The Rayleigh length is defined as the distance for which the beam radius is smaller or equal to √2 times the radius at the waist. So, when a focal length is small compared to the incident beam size, the depth of field tends to be small and vice-versa. Finally, M² corresponds to the quality factor. Basically, it's a measurement of how well your beam behaves when compared to a perfectly shaped theoretical TEM₀₀ Gaussian beam. A value of "1" is considered perfect and the farther from that value you are, the less it is.
Click toenlarge
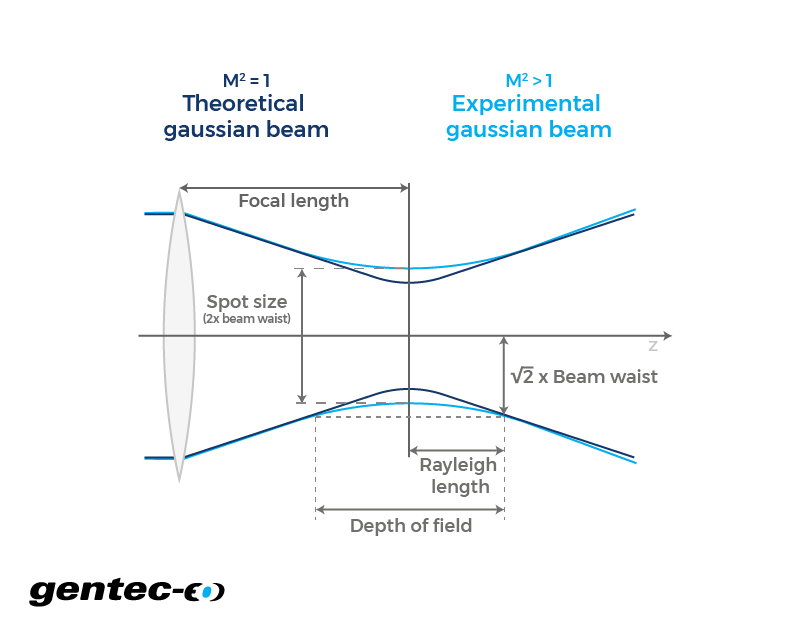
Formulas for spot size, beam diameter and depth of field
It is assumed here that once the laser beam passes the lens, it is going through a homogenous isotropic continuous medium in perpetuity. It is also supposed that the laser only emits one specific wavelength and that it can be represented as a TEM₀₀ Gaussian beam. Besides the beam, the lens is considered to be perfect and thin. So, its surface has no asperity and the focal length is identical across its entire surface. Our calculations come from the paraxial approximation of Helmholtz equation and the thin lenses approximations. Also, the incident beam is considered to be perfectly collimated on the lens. Therefore, the waist position on the z axis coincides with the focal point and is at focal length from the lens. Finally, these equations are not accurate to calculate the beam diameter in a far field. In that case, you should use our divergence calculator with the initial diameter being punctual (0) and directly at the focal plane.
Ref: Saleh, B. E. A., & Teich, M. C. (2007). Fundamentals of Photonics (2nd ed.). Wiley-Interscience.
Right-clickto copy
Right-clickto copy
Right-clickto copy