Peak power and peak power density
Calculate laser peak power and peak power density for your pulsed laser from your energy per pulse or average power.
How does the laser peak power calculator work?
Peak power is a concept that is only useful when you think about pulsed lasers. In a continuous wave laser, there are small fluctuations, but basically, one could say that the minimum, average and maximum power of a continuous wave laser are the same. In a pulsed one, each small burst of energy is separated by down times where no light is emitted. So the minimum power is usually 0 W and the maximum power is at peak when the intensity reaches its maximum value. To calculate the peak power of a laser beam, you would have to divide the energy in each pulse by the duration of the pulse (also known as pulse width). Then, to find the peak power density, you only have to divide the peak power by the area of the beam's cross-section at a given distance. Also, in the case where someone already knows the average power of its laser, we can find the energy per pulse by dividing it by the repetition rate. The laser power density is also a value that would affect how a material reacts to it. Of course, a pulsed laser could damage a surface by the accumulation of total energy over time, but that would be related to its average power. Because the energy transmission isn't done in a continuous manner, the surface could also be damaged during each pulse. It would happen if the energy in a single pulse is too high for the material to absorb and diffuse it while maintaining its physical integrity. So, each pulse would blast off a part of the surface.
Click toenlarge

Formulas for peak power and peak power density
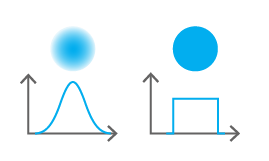
The formulas describe the behavior of a theoretical flat-top or a perfectly Gaussian laser beam. In such, they represent an approximation of the values one would obtain in real conditions. Also, there are multiple methods one can use to measure the diameter of a Gaussian beam. The reason for this mainly comes from the fact that its theoretical value only reaches 0 when the radius reaches infinity. Therefore, the beam would have an infinite diameter. So, we chose to use the method where it is measured using the 1/e² parameter. At this point, the beam diameter is approximately 1.699 times the full diameter measured at half the maximum of a Gaussian function (FWHM). At 1/e², it represents approximately 86.5% of the total power. Note that for a flat-top beam, the formulas are used just as is, but for a Gaussian beam, there is a factor 2 that multiplies the right hand part of these equations.
Right-clickto copy
Right-clickto copy
Right-clickto copy
Right-clickto copy