The beginner’s guide to laser beam quality and M2 measurement

Laser theory teaches us that by design, most laser beam should have a Gaussian beam shape. The fundamental mode of the Gaussian beam (TEM₀₀) is an ideal that most laser system designers want to achieve for three main reasons:

1. Its intensity is maximal on the optical axis, which makes the optical power and intensity nicely concentrated;
2. It has the lowest divergence, so it is often treated as a thin ray of light that doesn’t widen;
3. It is diffraction-limited, which means that when focused, the beam waist is the smallest that can be obtained for that specific wavelength.

But in real life, nothing is perfect, and a pure Gaussian beam with a TEM₀₀ profile and a bell-shaped curve that spreads on infinitely is, unfortunately, never achieved.

You might wonder (and many people do), how close is your real-life laser to perfection? In this guide, we will introduce you to the concept of laser beam quality measurement with the M2 parameter, which quantifies the laser beam quality, and how to measure M2 for a real laser.

How do we define laser beam quality?

The first lasers were made in the 60s, but it wasn’t until the early 90s that Anthony E. Siegman proposed a standard measurement for how close a laser beam is to this ideal Gaussian beam or, in other words, the measurement of laser beam quality.

Basically, it comes down to checking how your real beam waist and divergence compare to the ideal Gaussian beam at the same wavelength.

The beam parameter product (BPP) is one laser beam quality indicator that certain people use, and it is defined as the product of the beam’s smallest radius (the beam waist radius, w₀) with the beam’s divergence half-angle (θ), measured at the far field. Units of measurement for BPP are mm-mrad:

BPP = θ w₀

Ideal Gaussian beams have the smallest BPP for a given wavelength. Since we know that θ_ideal = λ / (π w_0,ideal ), the BPP for an ideal beam simplifies to BPP_ideal= λ / π. While it is simple to calculate, the BPP is not the best tool to compare one laser with another, because its ideal value changes with the wavelength.

Laser specifications change over time for many reasons and it causes problems accross all industries. Learn about how laser output measurement solves numerous problems in YOUR industry. Download the guide below.

Gentec-EO's high-accuracy laser beam measurement instruments help engineers, scientists and technicians in all sorts of laser applications from the factory to the hospital, laboratory and research center. Learn about our solutions for these measurement types:

• Laser power meters
• Laser energy meters
• Laser beam profilers
• Terahertz power meters

What Siegman proposed is to use a dimensionless value for laser beam quality, by dividing a real laser’s BPP with the one from an ideal laser. We therefore obtain a ratio that indicates how close your laser beam is to the perfect Gaussian beam, and Siegman called this value M² (pronounced m-squared).

M² = π θ w₀ / λ

One nice thing about M² is that it is dimensionless (i.e. no units of measurement), which makes it simpler to compare different lasers. On the other hand, it’s a bit counter-intuitive, but lower values of M² indicate better quality than higher values. In fact, the best possible result is M² = 1, and as the value of M² increases, the quality of the laser decreases. To have a better grasp on how quickly the M² value can affect your spot size or beam diameter in the near field, check this calculator of ours, it is an efficient and instructive test bench.

Why is it important to know the beam quality of your laser?

Once the M² factor is defined, it is possible to inject it back into the equations for generalized Gaussian beam propagation. When you know your laser’s M² factor, these equations describe how your REAL laser beam propagates, how tightly it can be focused and how quickly it diverges.

Meaning, is it Death Star material or more of a “I can annoy you with my laser pointer” material. But, in more practical terms, focusing laser beams tightly is particularly important when the application at hand is imaging, manufacturing, or destroying planets at a distance. Smaller beam waists mean having a better resolution as well as the possibility of reaching higher power densities.

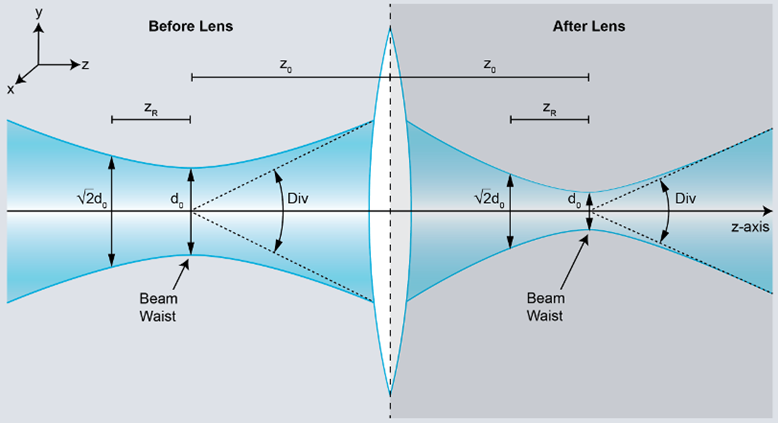
It is also common practice in systems with fiber optics to look for lasers with an M² close to 1 to allow for good coupling with single-mode fibers. The beam waist for a real beam is defined as:

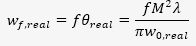
As you can see in the equation above, laser beams with a lower value of M² can be focused more tightly than lasers with a high M².

Beam quality measurement will also allow you to know how your laser beam will diverge. When you know your beam’s divergence, you can predict the size of your laser beam at pretty much any point in space. The beam radius for a real beam is defined as:

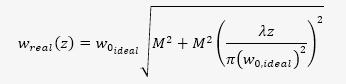
And the divergence in the far field for a real laser is defined as:

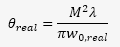
In the equation above, you can see that lasers with a high M² diverge more rapidly than lasers with a low M². Laser manufacturers like to provide the M² factor in their specifications because it gives the users an idea of how easy it will be to work with their laser.

How is M² calculated?

Siegman’s proposal became popular because of its simplicity, but experimentally it isn’t so straightforward, and some uncertainties arise from these principles. For example, if you want to measure the waist radius in the lab, how can you be sure that your measurement device is positioned exactly at the focus?

And how far do you need to go to be in the far field to measure the divergence? Are these two data points enough? The folks at the International Organization for Standardization, or ISO, decided to put an end to all this confusion, so they wrote a norm explaining how to measure and calculate M² properly: ISO 11146.

The ISO norm explains a method to calculate M² from a set of beam diameter measurements, in a way that minimizes sources of error. Here are the main steps:

1. Start with a collimated beam
2. Focus it with an aberration-free lens
3. Measure the diameter of the beam at various positions around the focal point: take at least 10 data points, approximately half within the first Rayleigh distance of the focal point, and the other half beyond 2 Rayleigh lengths.
   
   
   
4. Use the regression equations detailed in the norm to fit a hyperbola to your data points for both the X and Y axes. This improves the accuracy of the calculation by minimizing measurement error.
5. From this fit, extract the values for θ, w₀, z_R and M² for each axis.

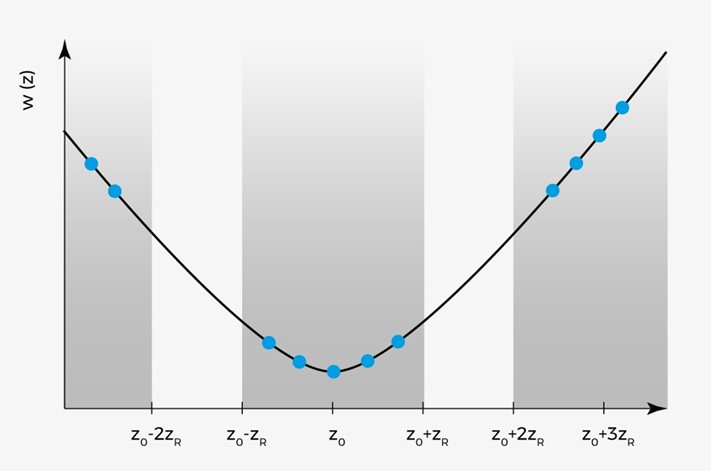
The ISO norm also states a few extra rules about the measurement of diameters (especially when using array sensors such as CCD or CMOS sensors):

• Make sure that you have at least 10 pixels within the diameter.
• Use a region of interest of 3 times the diameter.
• Calculate the diameter using the D4σ definition (second moment width).
• Always remove the background noise before taking a measurement.

What equipment do you need to measure laser beam quality?

At the most basic level, all you need is a lens, a beam profiler and a ruler. You can read our application note that explains step-by-step how to measure beam profile quality with these basic tools and calculate the laser beam quality result using our free software.

Although it is inexpensive, this method is time-consuming, so you have to wish that your laser is stable enough so that its M² value doesn’t fluctuate while you are taking the various diameter measurements! A simple way to increase the acquisition speed is to mount the beam profiler on a motorized translation stage and automate the acquisition.

In the moving stage case, setting up your system and automation routine can take a while, so you can save a lot of time and effort, because we did it all for you already! Our Beamage-M2 automated laser beam quality measurement system goes a few steps further than what was described above and it is so easy to set up that you can start measuring M² values in a few minutes the first time, and in less than a minute once you get it going.

Is M² measurement the right thing for you?

Now that you know more about laser beam quality measurement, you will have a better idea of whether it is actually what you need to measure. Keep in mind that M² is an indicator of how close your laser beam is to the ideal TEM₀₀ Gaussian beam.

If you are trying to develop a laser with nondiffractive beams like Bessel beams, or higher-order Gaussian beams with donut profiles, or more simply a top-hat beam, M² is not an indicator that you should be aiming for.  It would not really make sense nor be of great usefulness. For some applications, knowing only the beam divergence would be enough and far more relevant.

That’s it! You now understand the fundamentals of M² measurement… Any questions? Feel free to comment below or contact us, we will be happy to answer!