The beginner's guide on spot size of laser beam
Monday, July 10, 2023
When someone asks me how to measure the spot size of their laser beam, I often answer with a few questions, because this type of measurement is not as simple as it can appear at first glance, especially if you want to do it with precision and rigor.
Here are my usual questions/answers.
- Do you want to measure the focal spot or the beam diameter?
- Which beam diameter definition do you want to use?
- Do you have the appropriate instruments?
Let’s look at each one and why I ask them.
Do you want to measure the focal spot size or the beam diameter?
Without the context of what someone wishes to achieve with a measurement, it is easy to get lost in translation.
For some people, the expression spot size of a laser beam means its smallest diameter at the focal plane when focused by a lens, whereas for other people they mean the laser beam’s diameter when it exits the laser, or at any other place where they need to measure it.
It is important to make a distinction between the two cases because the approach to measurement is different.
Actually, we made two free calculators that are easy to use and fit these different scenarios. They will also provide some complementary information regarding their measurement definition on top of being proper calculation tools.
For calculating your spot size at the focal plane, use the spot size and beam waist calculator. If the beam diameter is not exactly at the focal plane, you have two options. If you’re still close to the focal plane, we’re talking distances that are about the Rayleigh range here, you should still use the same calculator as suggested above. If you’re in a far field though, go with our beam divergence and diameter calculator instead.
Laser output measurement solves numerous problems for organizations across all industries. Download the guide below. Gentec-EO's high-accuracy laser beam measurement instruments help engineers, scientists and technicians in all sorts of laser applications from the factory to the hospital, laboratory and research center. Learn about our solutions for these measurement types:
When a laser beam propagates along its optical path, its diameter is continually changing. If we consider the ideal case of a Gaussian beam, the beam width (or radius, w) along the propagation axis z is defined by the following equation:
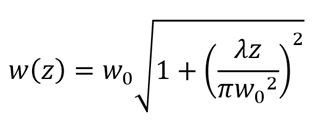
where w0 is the beam waist (the smallest radius of the Gaussian beam) and zR is the Rayleigh length:
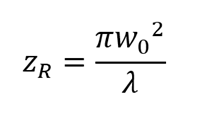
The beam diameter is simply twice the beam radius, and can be measured anywhere along the propagation axis.
When you focus a Gaussian beam with a lens of focal length f, the beam waist (or laser spot size equation) becomes:
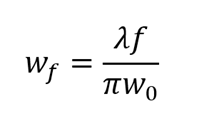
The focal spot size can therefore be very small, and when it is, the beam size varies very rapidly along the propagation axis. Measuring a focal spot size of laser beam is almost an art unto itself since it requires a very high degree of precision in the position of the sensor’s imaging plane and a means of adjusting this position to find the focal plane.
Since a focal spot measurement is basically a special case of laser beam diameter measurement, we will concentrate on the latter in this article.
Which beam diameter definition do you want to use?
There are three common beam diameter definitions: FWHM, 1/e2 and D4σ. Here is a quick overview of how they are calculated and how they are related.
FWHM (Full width at half-maximum)
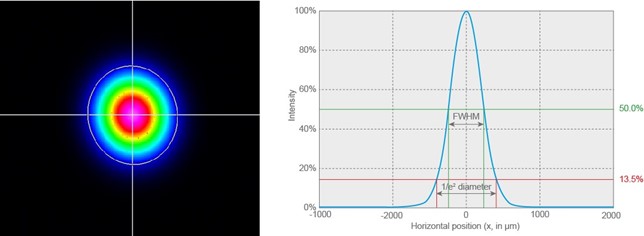
The full width at half-maximum, also called half-power beam width, is measured from the distribution curve of the beam’s intensity along a pre-defined axis, passing through the beam’s center, which is also usually its point of maximum intensity. The FWHM corresponds to the distance between the two points closest to the peak that have 50% of the maximum irradiance or intensity.
Some people prefer using other percentages of a beam’s maximum intensity to define its width. A common one is 13.5%, which leads us to our next beam diameter definition: 1/e2.
1/e2 (13.5% of maximum)
Although it might seem to be a weird choice of value, 1/e2 actually comes from a simplification. In the equation describing the Gaussian beam’s radial distribution,
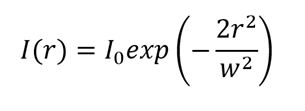
we can see that if we look at the point where the radius is equal to w (ergo at the theoretical beam width radius), then the intensity is 1/e2 times the maximum value:
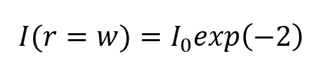
So, where does the 13.5% come from? Simply that e, Euler’s constant, is approximately equal to 2.71828, so 1/e^2 = 0.13534!
But how does this relate to the FWHM, would you ask? From the Gaussian beam equation, we can find the radius for which the intensity is half the maximum and isolate w:
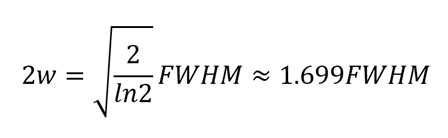
Since both the FWHM and the 1/e2 definitions are calculated from the intensity distribution along one axis, neither of them takes into account the overall beam profile. The following definition does exactly that.
D4σ (Second moment width)
This third definition for laser beam diameter is very commonly used, mainly due to the fact that its use is recommended by the ISO international standard for measuring beam widths (diameter), divergence angles and beam propagation ratios of laser beams.
Basically, the D4σ diameter is 4 times the standard deviation of the distribution of intensity along the major and minor axis of the beam. It is calculated from the second moment of the beam profile. For a perfect Gaussian beam with no noise in the measurement system, the measured diameters in 1/e2 definition and D4σ are identical.
The main drawback from this method is that if there is background noise in the measurement, the calculated diameter will be larger than the real value. This is why we recommend to always do a background subtraction before measuring a laser beam diameter.
Try our laser beam diameter calculator
Gentec-EO's beam diameter calculator is publicly available and free to use.
Do you have the appropriate instruments?
Knowing your laser is the first step towards acquiring the right laser beam profiler for your spot size measurement.
Wavelength range
Since your instrument is based on an array of detectors, it must be sensitive to your laser’s wavelength. If it isn’t, you will get no signal, therefore no measurement. In some cases, we might recommend beam profiling accessories such as UV converters or IR adaptors that use fluorescence or phosphorescence to convert your beam into visible wavelengths for which our cameras are sensitive.
If your wavelength is in a spectral region where our sensor is only slightly sensitive, then we might recommend using a filter that will block light from other wavelengths, reducing noise from the environment or unwanted sources.
Sensor dimension and pixel pitch
Before purchasing a laser beam profiling instrument, you should have a general idea of the beam size you will be measuring. You will need to know this to make sure that your sensor is large enough and also that the pixels are small enough.
We recommend a sensor size of at least 3 times the largest diameter. For the pixel pitch (or, equivalently, pixel size), we recommend that the smallest beam you will measure should fit within at least 10 pixels.
For example, if the sensor has a pixel pitch of 5.5 µm, you should not try to measure beams smaller than 55 µm with it.
Laser power and laser power density
The last parameter you will need to check is what laser power density hits your sensor. You can calculate this from your beam diameter and average power (even for pulsed beams) and add attenuation filters accordingly.
Even though the math is simple, it can be confusing if you’re not used to calculating it. To make it easier, we suggest you use our free calculators here again. Depending if your laser is pulsed or continuous, use one of these 3 calculators:
- Average power and power density for both types of lasers
- Peak power and peak power density for pulsed lasers
- Energy density / fluence for pulsed lasers
You must also take into consideration that the sensitivity of the laser beam profiler changes with the wavelength, and so does the saturation. To simplify your calculations, we provide curves for minimum and maximum power density for each of our beam profilers. Here is an example.
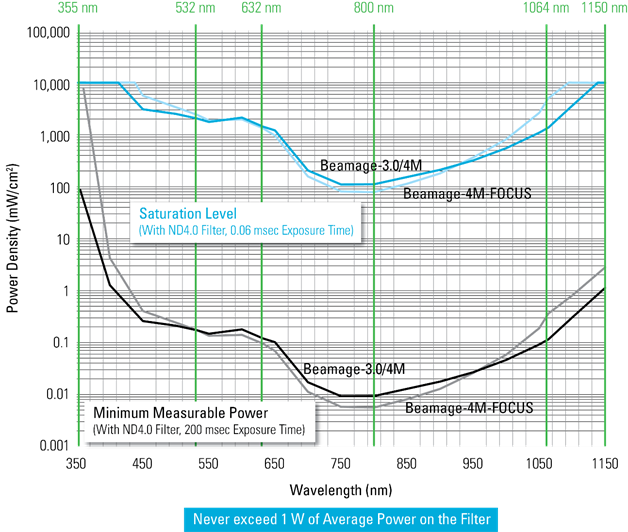
If the average power is above 1 W, you will have to sample your beam before using attenuation filters. Our product lineup includes a variety of beam samplers that can accommodate laser beams up to 1 kW.
If you don’t know the exact diameter and power of your laser, approximations will be fine because beam profilers have an adjustment in exposure time to compensate for variations in power density.
If you need help choosing a beam profiler and its accessories, don’t hesitate to contact us, we’ll be glad to help you out!
